9 データの概要と分布の把握
9.1 はじめに
データ分析においては、データの概要を把握するために、記述統計と呼ばれる分析をほぼ必ず行います。「ユーザーの年齢層は?」といった問いに答えるために、年齢の平均値や標準偏差といった要約統計量を計算することになります。
要約統計量は便利ですが、罠もあります。平均値などの数値を計算するだけだと、データの分布形状という重要な特徴を見逃してしまいます。
このページでは以下の3つの項目を解説します。
- 記述統計の基礎:データの代表値やばらつき度合いを数値で要約する方法。
- 数値の落とし穴:要約統計量だけではデータの特徴が見抜けない事例。
- 分布の可視化:データの分布を見るための可視化のテクニックについて。
このページで扱う内容はどんなデータ分析をする場合でも必ず意識しておくべき重要なものであり、データを手にしたら癖のように自然に行うというレベルになることが望ましいです。
9.2 データの要約と記述統計
手元にある大量のデータを分析する際、最初に行うべきことは、そのデータがどのような特徴を持っているかを把握することです。
大量のデータをそのまま眺めていても、全体像は見えてきません。そこで、データを代表する数値(平均値など)を計算したり、表やグラフを作ったりして、データを整理・要約します。このように、手持ちのデータの特徴を記述・要約する分析のことを記述統計(Descriptive Statistics)と呼びます。
記述統計において、データの性質をたった一つの数値で表したものを要約統計量(Summary Statistics)と呼びます。平均値や中央値、分散や最大値などは、要約統計量の代表例です。
このセクションでは、「タイタニック号の乗客データ」を使いながら、基本的な要約統計量の算出方法を解説します。
9.2.1 データの準備
まずは分析に使用するパッケージをインストールします。Console で以下の命令を実行して2つのパッケージをインストールします。
次に、タイタニックデータを読み込みます。
このデータセットには沈没時のタイタニック号の乗客の情報が記録されており、以下のような列があります。
- PassengerId:乗客ID
- Survived:生存状況(0=死亡、1=生存)
- Pclass:客室クラス(1=1等、2=2等、3=3等)
- Name:乗客の氏名
- Sex:乗客の性別(male=男性、female=女性)
- Age:乗客の年齢
- SibSp:タイタニック号に同乗している兄弟(Siblings)や配偶者(Spouses)の数
- Parch:タイタニック号に同乗している親(Parents)や子供(Children)の数
- Ticket:チケット番号
- Fare:旅客運賃
- Cabin:客室番号
- Embarked:出港地(C=Cherbourg:シェルブール、Q=Queenstown:クイーンズタウン、S=Southampton:サウサンプトン)
9.2.2 量的データの要約(要約統計量)
年齢や運賃のように、数値の大きさに意味があり、数値計算(合計値や平均値などの計算)ができるタイプのデータを量的データ(Quantitative Data)と呼びます。
量的データを要約する統計量は、主に「分布の中心(代表値)」と「分布の広がり(散布度)」の2種類に分類されます。
全体をざっと確認する summary()
Rで最もよく使われるのが summary() 関数です。これを使うと、主要な要約統計量を一度に確認できます。乗客の年齢の要約統計量を計算してみましょう。
summary(dat$Age)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.42 20.12 28.00 29.70 38.00 80.00 177出力の意味:
代表値(分布の中心)
- Median(中央値):値の大きさ順に並べたときに、ちょうど真ん中に来る値。
- Mean(平均値):データの合計値を個数で割った値。
散布度(分布の広がり)
- Min(最小値)や Max(最大値): データの範囲を示します。
- 1st Qu(第1四分位数)や 3rd Qu(第3四分位数): データを4等分したときの区切り値。
NA’s は欠損値(NA)の数です。
タイタニック号の乗客は平均29.7歳であり、乗客のうち半数は20.12歳から38歳の間だったこと、最高齢は80歳だったことなどがわかります。
統計量を個別に計算する
それぞれの要約統計量を個別に計算するための関数も見ていきましょう。
# --- 代表値(データ分布の中心位置) ---
# 平均値
mean(dat$Age, na.rm = TRUE)
## [1] 29.69912
# 中央値
median(dat$Age, na.rm = TRUE)
## [1] 28
# --- 散布度(データ分布の広がり) ---
# 分散 (Variance): データが平均からどれくらい離れているかの平均的な指標
var(dat$Age, na.rm = TRUE)
## [1] 211.0191
# 標準偏差 (Standard Deviation): 分散の平方根。元のデータと同じ単位(歳やドル)でばらつきを表す
sd(dat$Age, na.rm = TRUE)
## [1] 14.5265
# 範囲 (Range): 最小値と最大値を同時に返す
range(dat$Age, na.rm = TRUE)
## [1] 0.42 80.00
# --- その他 ---
# 合計 (Sum): 例えば「乗客全員が支払った運賃の総額」を知りたい時など
sum(dat$Fare)
## [1] 28693.95データに欠損値(NA)が含まれている場合、平均値などの計算結果は NA になります。これを防ぐために na.rm = TRUE というオプションを指定します。
Age 列は NA を含む(年齢データを持たない乗客の行がある)ので na.rm を TRUE にしていますが、Fare 列には NA が含まれていないので、最後の例ではオプションの指定は不要です。
9.2.3 質的データの要約(度数分布)
性別(男性/女性)や客室クラス(1等/2等/3等)のように、分類やカテゴリを表すデータを質的データ(Qualitative Data)と呼びます。質的データは量的データとは違い、数値を足したり割ったりすることに意味がないため、平均値などの計算は行いません。
代わりに、各カテゴリに何件のデータがあるかを数える度数(Frequency)を確認します。
# 性別ごとの人数(度数)を数える
table(dat$Sex)
##
## female male
## 314 577
# 客室クラスごとの人数を数える
table(dat$Pclass)
##
## 1 2 3
## 216 184 491女性より男性が多いこと、3等客室の数が最も多いことなどがわかります。
人数だけでなく、「全体の何%か」という相対度数(割合)を知るには、table() の結果を prop.table() 関数に渡します。
# 客室クラスの割合を計算する
tab = table(dat$Pclass)
prop.table(tab)
##
## 1 2 3
## 0.2424242 0.2065095 0.5510662これにより、例えば「3等客室の乗客が全体の半数以上(55.1%)を占めている」といった特徴を掴むことができます。
確認問題:男女の割合を計算してください。
(解答:女性35.2%、男性64.8%)
9.2.4 グループごとの要約(層別分析)
データの全体像を把握したら、次はデータを特定の条件で分けて比較します。これを層別分析といいます。「乗客の年齢層は客室のクラスによって違うか?」「男性と女性で死亡率に違いはあったか?」といった疑問に答えるプロセスです。
さまざまな統計量をまとめて算出する describeBy()
psych パッケージの describeBy() 関数を使うと、グループごとの記述統計量を一括で算出できます。
- チルダ記号(~)を使い、
集計したい列名 ~ グループの列名という形式(モデル式)で第一引数を指定します。 - data 引数にデータフレームを渡します。
library(psych)
# 客室クラス(Pclass)ごとに年齢(Age)を集計する
describeBy(Age ~ Pclass, data = dat)
##
## Descriptive statistics by group
## Pclass: 1
## vars n mean sd median trimmed mad min max range skew kurtosis se
## Age 1 186 38.23 14.8 37 37.98 16.31 0.92 80 79.08 0.12 -0.41 1.09
## ------------------------------------------------------------
## Pclass: 2
## vars n mean sd median trimmed mad min max range skew kurtosis se
## Age 1 173 29.88 14 29 29.87 10.38 0.67 70 69.33 0.13 0.17 1.06
## ------------------------------------------------------------
## Pclass: 3
## vars n mean sd median trimmed mad min max range skew kurtosis se
## Age 1 355 25.14 12.5 24 24.84 10.38 0.42 74 73.58 0.48 0.94 0.66Pclass の値ごとに、Age の各種の要約統計量が表示されています。mean の箇所を見ると、乗客の平均年齢は1等客室が最も高く38.2歳であり、3等客室は最も低く25.1歳であることがわかります。
describeBy() で出力される値のリスト:
- n: number of valid cases(データ件数)
- mean: mean(平均値)
- sd: standard deviation(標準偏差)
- median: median(中央値)
- trimmed: trimmed mean (with trim defaulting to .1)(トリム平均)
- mad: median absolute deviation (from the median)(中央絶対偏差)
- min: minimum(最小値)
- max: maximum(最大値)
- range: range(範囲/レンジ)
- skew: skewness(歪度:わいど)
- kurtosis: kurtosis(尖度:せんど)
- se: standard error(標準誤差)
describeBy() 関数では、複数のグループの組み合わせごとに集計を行うこともできます。
集計したい列名 ~ グループの列名1 + グループの列名2という式で指定します。- 例:
Age ~ Pclass + Sex(客室クラスと性別の組み合わせごとに年齢を集計)
特定の統計量をピンポイントで集計する aggregate()
psych::describeBy() 関数は多くの統計量を出力しますが、特定の値(たとえば平均値)だけを計算できればそれでよいという場合も多くあります。
そのような場合にはRの標準関数である aggregate() 関数が便利です。
集計したい列名 ~ グループの列名という式(モデル式)で集計方法を指定します。- data 引数にデータフレームを渡します。
- FUN 引数に集計に用いる関数(mean や sd など)を指定します。
# 性別ごとに年齢を平均値(mean)で集計する
aggregate(Age ~ Sex, data = dat, FUN = mean)
## Sex Age
## 1 female 27.91571
## 2 male 30.72664複数のグループ変数を組み合わせた集計(クロス集計)も簡単に行えます。以下の例では、客室クラスごとに、男女で分けて平均年齢を計算しています。
aggregate(Age ~ Pclass + Sex, data = dat, FUN = mean)
## Pclass Sex Age
## 1 1 female 34.61176
## 2 2 female 28.72297
## 3 3 female 21.75000
## 4 1 male 41.28139
## 5 2 male 30.74071
## 6 3 male 26.50759どちらの性別でも、高級なクラスの客室ほど年齢が高いことがわかります。
なお、モデル式を使って集計方法を指定した場合、欠損値を含む行は自動で削除されます。したがって、na.rm = TRUE という指定は不要です。
9.2.5 発展:平均値とデータの件数を同時に確認する
平均値などの統計量を解釈する際に重要なのが「その値は何人分のデータに基づいているか(サンプルサイズ)」を確認することです。 例えば、生存率100%という結果が出ても、そのグループの該当者がたった1人しかいなければ、それが一般的な傾向なのか偶然なのかが判断できません。
要約統計量と一緒にデータの件数も算出する2つの方法を紹介します。
標準機能(aggregate)を使う方法
aggregate() 関数の FUN 引数には、mean などの元からある関数だけでなく、自分で作った関数を指定することができます。 これを利用して、「平均値」と「データの長さ(length=件数)」をセットで計算させます。
# FUN = function(x) { ... } の中で、計算したい指標を c() でまとめる
# mean = 平均値, n = 件数(length)
aggregate(Age ~ Pclass, data = dat, FUN = function(x) c(mean = mean(x), n = length(x)))
## Pclass Age.mean Age.n
## 1 1 38.23344 186.00000
## 2 2 29.87763 173.00000
## 3 3 25.14062 355.00000Age.n の箇所がデータの件数(NA を除いたデータの件数)です。
dplyr パッケージを使う方法
より柔軟な集計を行いたい場合、データ操作に特化した dplyr パッケージを使うのが効果的です。 この場合は複数の要約統計量をまとめて算出できます。
以下の例では年齢の平均値と標準偏差、そしてデータ件数を客席クラスごとに計算しています。
library(dplyr)
df = dat %>%
group_by(Pclass) %>% # 客室クラスでグループ化
summarise( # グループごとに要約値を計算
Age.Mean = mean(Age, na.rm = TRUE), # 年齢の平均値
Age.SD = sd(Age, na.rm = TRUE), # 年齢の標準偏差
N = n(), # データ件数(dplyrでは length の代わりに n() を使う)
N.Age = sum(!is.na(Age)), # 要約統計量の計算に使われたデータ件数
.groups = "drop" # グループ化解除の指定(おまじない)
)
print(df)
## # A tibble: 3 × 5
## Pclass Age.Mean Age.SD N N.Age
## <int> <dbl> <dbl> <int> <int>
## 1 1 38.2 14.8 216 186
## 2 2 29.9 14.0 184 173
## 3 3 25.1 12.5 491 355- データ件数は n() で得られます。ただし、この値はグループごとのデータの件数を表現しており、Age の値が NAである行も含めた件数です。(
table(dat$Pclass)の計算結果と一致します。) - 平均値と標準偏差を計算する際は Age が NA であるデータは省かれています。要約統計量の計算に使われたデータの件数を調べるには、
sum(!is.na(Age))(欠損値ではないAgeの値の行数の合計)を計算すれば良いです。こちらの値は上で aggregate() 関数を使った場合の Age.n の値と一致しています。
9.2.6 確認問題:要約統計量の解釈
1等客室(Pclass:1)と3等客室(Pclass:3)の運賃(Fare)について、それぞれの平均値・中央値・標準偏差を計算してください。
そして、それぞれの要約統計量を比較し、タイタニック号の運賃にはどのような特徴があるのかを、標準偏差の値や、平均値と中央値の差などの観点から説明してください。
解答と解説(クリックして展開)
# describeBy関数を使う場合
result = psych::describeBy(Fare ~ Pclass, data = dat)
# dplyrでやる場合
library(dplyr)
result = dat %>%
filter(Pclass %in% c(1, 3)) %>% # 1と3だけを抽出
group_by(Pclass) %>%
summarise(
Fare.Mean = mean(Fare, na.rm = TRUE), # 平均値
Fare.Median = median(Fare, na.rm = TRUE), # 中央値
Fare.SD = sd(Fare, na.rm = TRUE), # 標準偏差
.groups = "drop"
)
print(result)
## # A tibble: 2 × 4
## Pclass Fare.Mean Fare.Median Fare.SD
## <int> <dbl> <dbl> <dbl>
## 1 1 84.2 60.3 78.4
## 2 3 13.7 8.05 11.8
# 個別に計算する場合
# 1等客室のデータだけを抽出
d1 = subset(dat, Pclass == 1)
mean(d1$Fare) # 平均値
## [1] 84.15469
median(d1$Fare) # 中央値
## [1] 60.2875
sd(d1$Fare) # 標準偏差
## [1] 78.38037
# 3等客室も同様に計算...
- 1等客室は平均$84.15、3等客室は平均$13.7であり、運賃は1等客室の方が遥かに高額。
- 3等客室は標準偏差が比較的小さく(11.8)、多くの客は平均値に近い金額を支払っている。
- 1等客室の運賃は標準偏差が大きい(78.4)。つまり、運賃価格のばらつきが大きい。また、1等客室は平均値が中央値よりも大幅に高い。このことから、一部の超高額な客室運賃によって平均値が引き上げられていることが分かる。
9.2.7 確認問題:層別の生存率
男性と女性で生存率に違いはあったのでしょうか?
- 生存率(生存状況 Survive の値の平均値)を性別ごとに計算してください。
- 性別ごとの生存率についてさらに詳細に検討するため、性別と客席クラスの組み合わせごとに生存率を計算してください。
- 得られた結果から、沈没時に何が起こっていたかを推測してください。
解答と解説(クリックして展開)
# 1. 性別ごとの生存率
aggregate(Survived ~ Sex, data = dat, FUN = mean)
## Sex Survived
## 1 female 0.7420382
## 2 male 0.1889081
# 2. 性別 × 客室クラスごとの生存率
aggregate(Survived ~ Pclass + Sex, data = dat, FUN = mean)
## Pclass Sex Survived
## 1 1 female 0.9680851
## 2 2 female 0.9210526
## 3 3 female 0.5000000
## 4 1 male 0.3688525
## 5 2 male 0.1574074
## 6 3 male 0.1354467
- Survived の値は死亡が0、生存が1なので、平均値を計算すればそれが生存率の値になります。
- 全体としては、女性の生存率は74.2%、男性の生存率は18.9%であり、女性の方が圧倒的に生存率が高くなっています。
- 同じ女性でも、1等客室と2等客室の客は9割以上の生存率ですが、3等客室では5割の生存率となっています。
- 生存率がこのような結果になった背景については史実を調べてみてください。
9.3 要約統計量の罠
上のセクションでは要約統計量(平均値や標準偏差)がいかに便利かを学びました。しかし、データ分析の世界には「数値計算だけで分析を終わらせてはいけない」という鉄則があります。
要約統計量は大量のデータをたった一つの数字に圧縮した結果です。情報の圧縮には「情報の欠落」が必ず伴います。時には、その欠落した部分に重要な情報が含まれていることがあります。
このセクションでは、要約統計量だけしか見ないことの問題点と、それを防ぐための可視化の重要性について解説します。
9.3.1 同じ統計量、違うグラフ:アンスコムの例
「平均値、分散、相関係数。これらが全て同じなら、それは同じようなデータだ」と思うかもしれません。その直感を覆す有名な例が、1973年に統計学者フランシス・アンスコムが提示した「アンスコムの例(Anscombe’s quartet)」です。
Rには、このデータが anscombe という名前で標準搭載されています。
統計量を確認する
このデータセットには4つのグループ、計8つの変数が含まれます。
- グループ1: x1, y1
- グループ2: x2, y2
- グループ3: x3, y3
- グループ4: x4, y4
まずは、このデータセットに含まれる4つのグループごとにXやYの平均値と分散、そしてXとYの相関係数を計算してみます。
なお、anscombe データはワイド形式になっているので、整然データの形式に変換しています(この変換処理は少しややこしいので読み飛ばしてしまっても構いません)。
library(tidyverse)
# データの読み込み
data(anscombe)
# anscombeデータセットはワイド形式なので、
# tidyverse で扱えるロング形式(整然データ形式)に変換する
anscombe_tidy = anscombe %>%
mutate(id = row_number()) %>%
pivot_longer(cols = -id, names_to = "key", values_to = "val") %>%
mutate(variable = str_sub(key, 1, 1), group = str_sub(key, 2, 2)) %>%
select(-key) %>%
pivot_wider(names_from = variable, values_from = val)
# 要約統計量(平均・分散・相関)の計算
anscombe_stats = anscombe_tidy %>%
group_by(group) %>%
summarise(
MeanX = mean(x),
VarX = var(x),
MeanY = mean(y),
VarY = var(y),
CorXY = cor(x, y)
)
# 結果
print(anscombe_stats)
## # A tibble: 4 × 6
## group MeanX VarX MeanY VarY CorXY
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 9 11 7.50 4.13 0.816
## 2 2 9 11 7.50 4.13 0.816
## 3 3 9 11 7.5 4.12 0.816
## 4 4 9 11 7.50 4.12 0.817要約統計量を計算した結果、どのグループも、XやYの平均値や分散、そしてX-Yの相関がほぼ同じ値であることがわかります。したがって、これらの数値を見る限り、「この4つのグループはほぼ同じデータ」だと結論したくなります。
グラフにして正体を見る
しかし、実際のデータを図で表示してみると、これら4グループは全く異なる性質を持っていることが明らかになります。
# グループごとにXとYの散布図を作成
ggplot(anscombe_tidy, aes(x = x, y = y)) +
geom_point(color = "gray20", size = 2) +
geom_smooth(method = "lm", se = FALSE, color = "#88b5d3") + # 回帰直線
facet_wrap(~ group, labeller = label_both) + # グループごとにグラフを分割
theme_bw() +
labs(title = "アンスコムの例", subtitle = "要約統計量は同じだが実態は異なる例")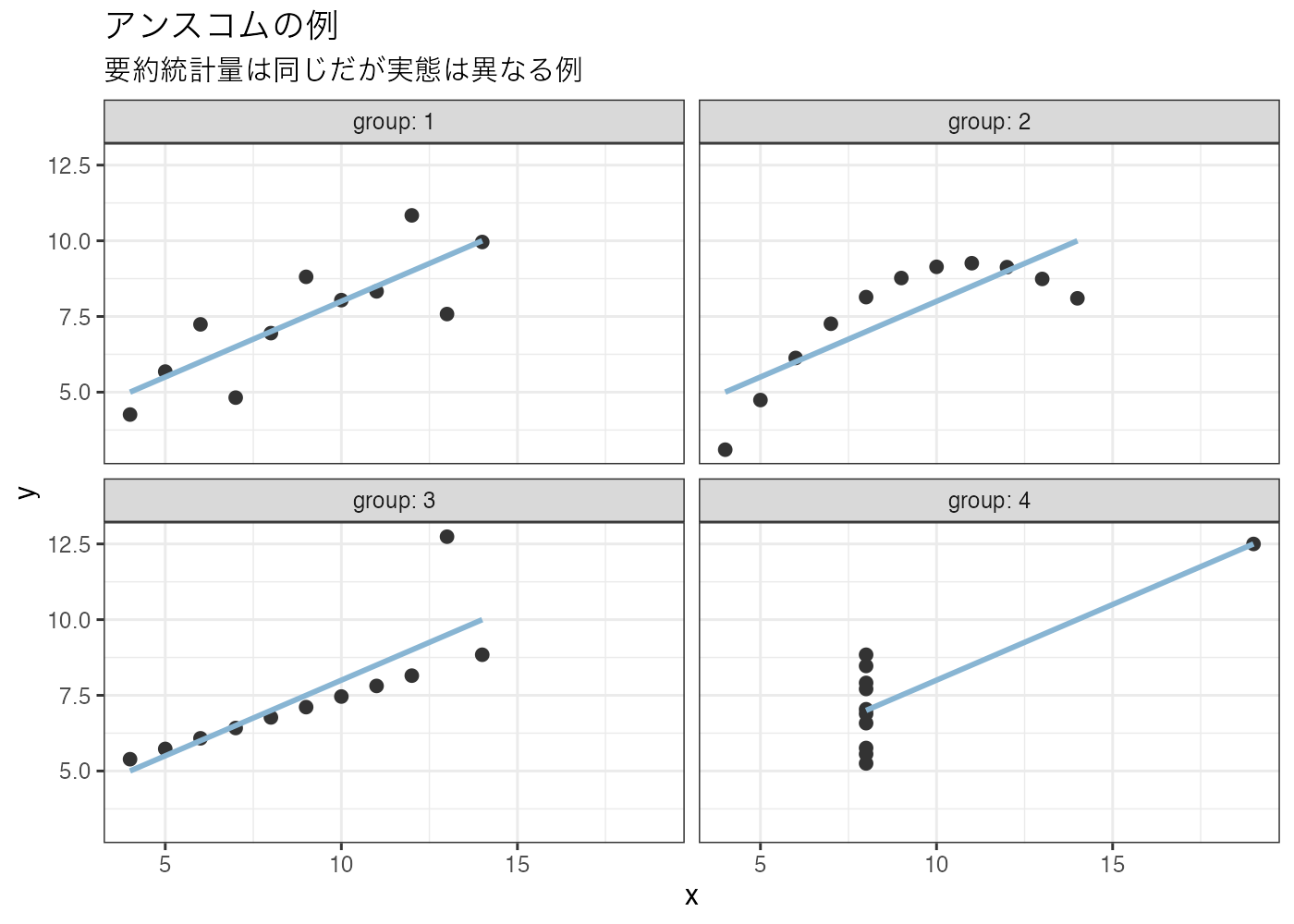
図の解説:
- Group 1: 一般的な相関関係に見えます。
- Group 2: 明らかな曲線を描いています。相関係数で評価するのは不適切です。
- Group 3: 綺麗な直線上にありますが、一つの外れ値が回帰直線を歪めています。
- Group 4: xの値はほとんど同じですが、一つの外れ値のせいで相関があるように見えています。
このように、要約統計量の数値は同じだったとしても、データの構造が全く別物である場合があり得るのです。
したがって、平均値や相関係数の数値だけを見てデータの性質を判断するのは危険です。データを得たら、まずは図を描いてデータの分布を目で確認する習慣をつけましょう。
9.3.2 多峰性分布:平均値が「存在しない値」を示す時
次に、「平均値」という代表値が全く代表的ではないケースを見てみましょう。 使用するのは、R標準の faithful データセットです。これはアメリカのイエローストーン国立公園にある「オールド・フェイスフル間欠泉」の噴出記録です。
次の噴出までの待ち時間は…
観光客のあなたは、次の噴出までの待ち時間(waiting)を知りたいとします。平均値を計算してみましょう。
「なるほど、平均71分待てばいいのか」とあなたは考えます。しかし、実際のデータの分布(ヒストグラム)を見てみると、異なる実態がわかります。
ヒストグラムによるデータの確認
# 平均値を計算しておく
avg = mean(faithful$waiting)
# ggplotで描画
fig = ggplot(faithful, aes(x = waiting)) +
geom_histogram(binwidth = 5, fill = "#88b5d3", color = "white") +
geom_vline(xintercept = avg, color = "orange", linewidth = 1) +
labs(x = "待ち時間 (分)", y = "度数 (回)") +
theme_classic()
plot(fig)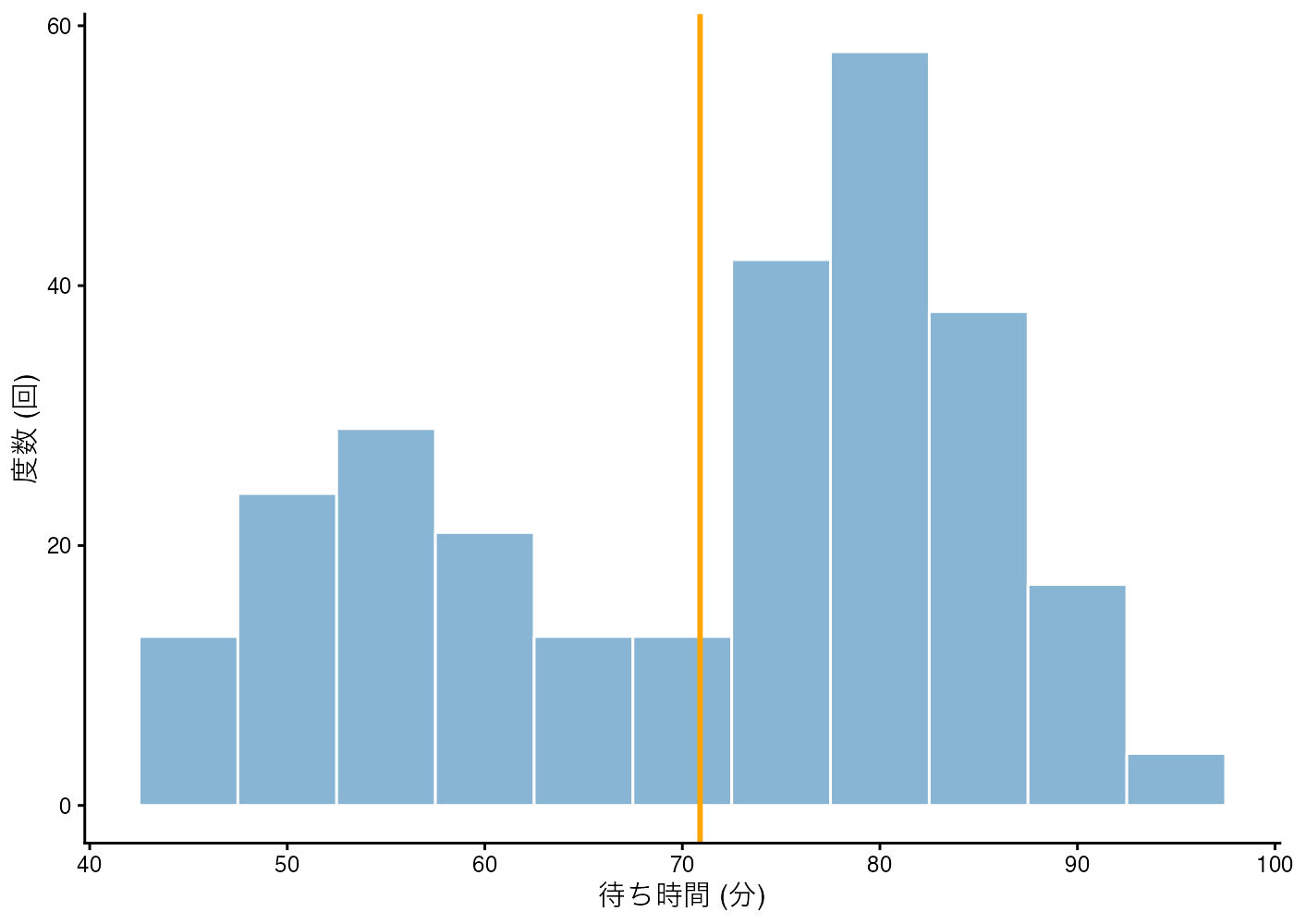
ヒストグラムを見ると、山が2つある二峰性分布(Bimodal Distribution)になっていることがわかります。
- 左の山:50分ほどの待ち時間(短い間隔)
- 右の山:80分ほどの待ち時間(長い間隔)
そして、計算した平均値(71分:オレンジ線)は、データの谷間(誰もいない場所)を指しています。 つまり、この間欠泉で「70分程度待つ」というケースは極めて稀なのです。
この例は、「平均値は最もよくある値(最頻値)を示すとは限らない」という典型的な例です。
9.3.3 要約統計量の罠:まとめ
このセクションでは「アンスコムの例」と「二峰性分布」を紹介しました。どちらも、要約統計量を計算しただけでデータがわかったと思うのは良くないことだと伝えています。
データ分析の最初のステップでは、要約統計量を計算するだけではなく、グラフを描いてデータの分布を確認することがとても重要です。
9.3.4 確認問題:平均値の罠
あるスタートアップ企業が「当社は平均年収2200万円です!」と求人を出しています。 しかし、実際の社員5人の年収データ(単位:万円)は以下の通りでした。
salary = c(300, 300, 400, 400, 9600)
- このデータの平均値と中央値をそれぞれ計算してください。
- あなたがこの会社に一般社員として入社する場合、自分の給料の目安として参考になるのは平均値と中央値のどちらの指標ですか? その理由とともに答えてください。
解答と解説(クリックして展開)
正解の選択と理由:
- 参考になる指標: 中央値(400万円)
- 理由:データの中に極端な外れ値(9600万円)が含まれており、平均値はその値に引きずられて実態よりも遥かに高くなっているから。中央値は外れ値の影響を受けにくく(ロバスト)、多数の社員の実際の給料の値を反映している。
9.3.5 確認問題:平均値と中央値
あるECサイトで、2つの商品(商品A、商品B)のカスタマーレビュー(5点満点)のデータを分析しています。 それぞれのレビューデータは以下の通りです。
問い:
- 商品Aと商品Bについて、それぞれの平均値と中央値を計算してください。
- 計算された数値だけを見た場合、この2つの商品は区別できますか?
- ビジネスの観点から見て、商品Bはどのような性質の商品だと言えますか?「ばらつき」や「顧客の反応」という言葉を使って考察してください。
- どのような値を計算すれば商品AとBの区別ができるでしょうか?
解答と解説(クリックして展開)
product_A = c(2, 3, 3, 3, 3, 4)
product_B = c(1, 1, 1, 5, 5, 5)
# 商品A
mean(product_A)
## [1] 3
median(product_A)
## [1] 3
# 商品B
mean(product_B)
## [1] 3
median(product_B)
## [1] 3考察と解説:
- 数値での区別:平均値も中央値も、両方とも「3」で完全に一致します。つまり、この2つの指標だけを見ていると、商品Aと商品Bは「全く同じような評価の商品」に見えてしまい、区別がつきません。
- 商品Bの性質(ビジネス的考察):商品Aが「全員が可もなく不可もなく(3点付近)」と感じているのに対し、商品Bは「絶賛(5点)」する人と「低評価(1点)」する人に真っ二つに分かれています。 ビジネス的には、商品Bは「熱狂的なファンがいるが、アンチも多い賛否両論な商品」あるいは「人を選ぶ尖った商品」だと言えます。要するに、商品Bは顧客の反応のばらつきが大きいのです。
- どのような値を計算すればいいか:散布度の指標(分散や最大・最小値など)を使えば、ばらつきの大きさを調べることができます。
先ほどの平均年収の確認問題のように、「平均値と中央値がズレていれば分布が歪んでいる」という事実は有名です。しかし、かといって、「平均値と中央値が一致していれば普通の分布(正規分布など)である」とも限らないのです。
量的データの要約(要約統計量)の箇所で書いたように、要約統計量には「代表値」と「散布度」があります。今回の問題のケースでは、平均値や中央値などの代表値だけではなく、分散や最大・最小値などの散布度も計算していれば、商品AとBの違いが要約統計量の値から区別できます(商品Bの方が散布度 = 分布のばらつき度合いが大きい)。
9.4 分布形状を確認しやすい可視化のテクニック
量的データを記述する際は「要約統計量」と「具体的な分布の形」の両方が重要であることをここまでに確認しました。では、どうすればその両方を効果的に表現することができるでしょうか?
このセクションではデータを的確に記述するための作図のテクニックを紹介します。
9.4.1 データの準備
ここでは ggplot2 の diamonds データを使用します。データ量が多いため(約54000行)、元データからランダムに2000行を抽出したデータを作成して解説を進めます。
9.4.2 ヒストグラム:ビン幅(binwidth)の重要性
量的データの分布形状を最も手っ取り早く確認するにはヒストグラムを描くのが良いでしょう。ヒストグラムは連続する数値を「区間(ビン)」に区切り、その中にあるデータの個数を柱の高さで表したグラフです。
ヒストグラムはRの基本関数である hist() 関数で描画できます。ダイヤモンドデータのカラット(重さ)の分布を見てみましょう。
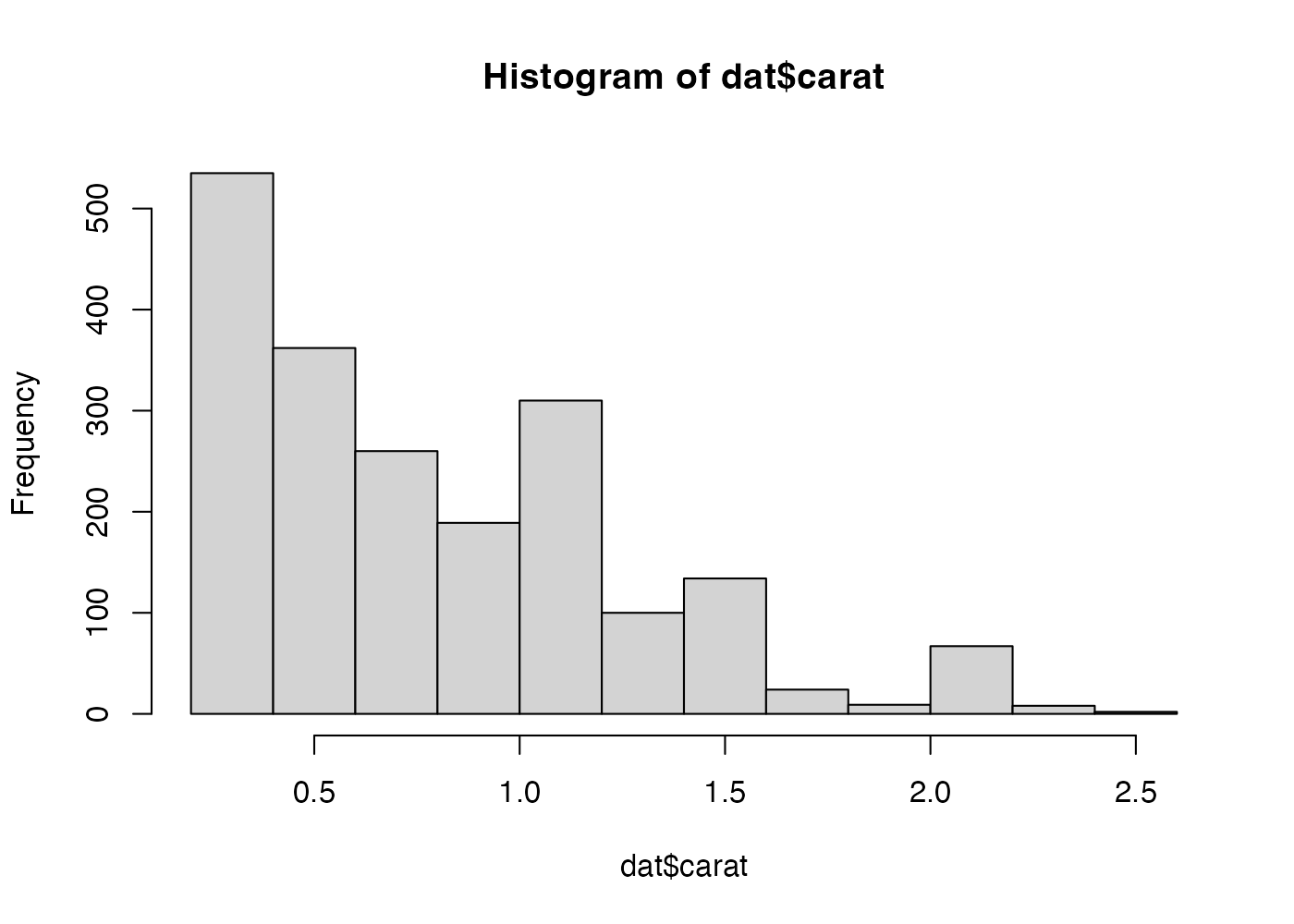
この図からは、重いダイヤほど数が少ないという、右下がりの分布が確認できます。
ビン幅を変えてみる
ヒストグラムを描く際には重要なパラメーターがあります。それがビンの幅です。ビン幅はどの範囲(区間)の値を同じ棒(グループ)とみなすかの値で、ヒストグラムのひとつひとつの棒の横幅に対応します。
hist() 関数では breaks 引数でビン幅(というより、棒の総数)を指定します。
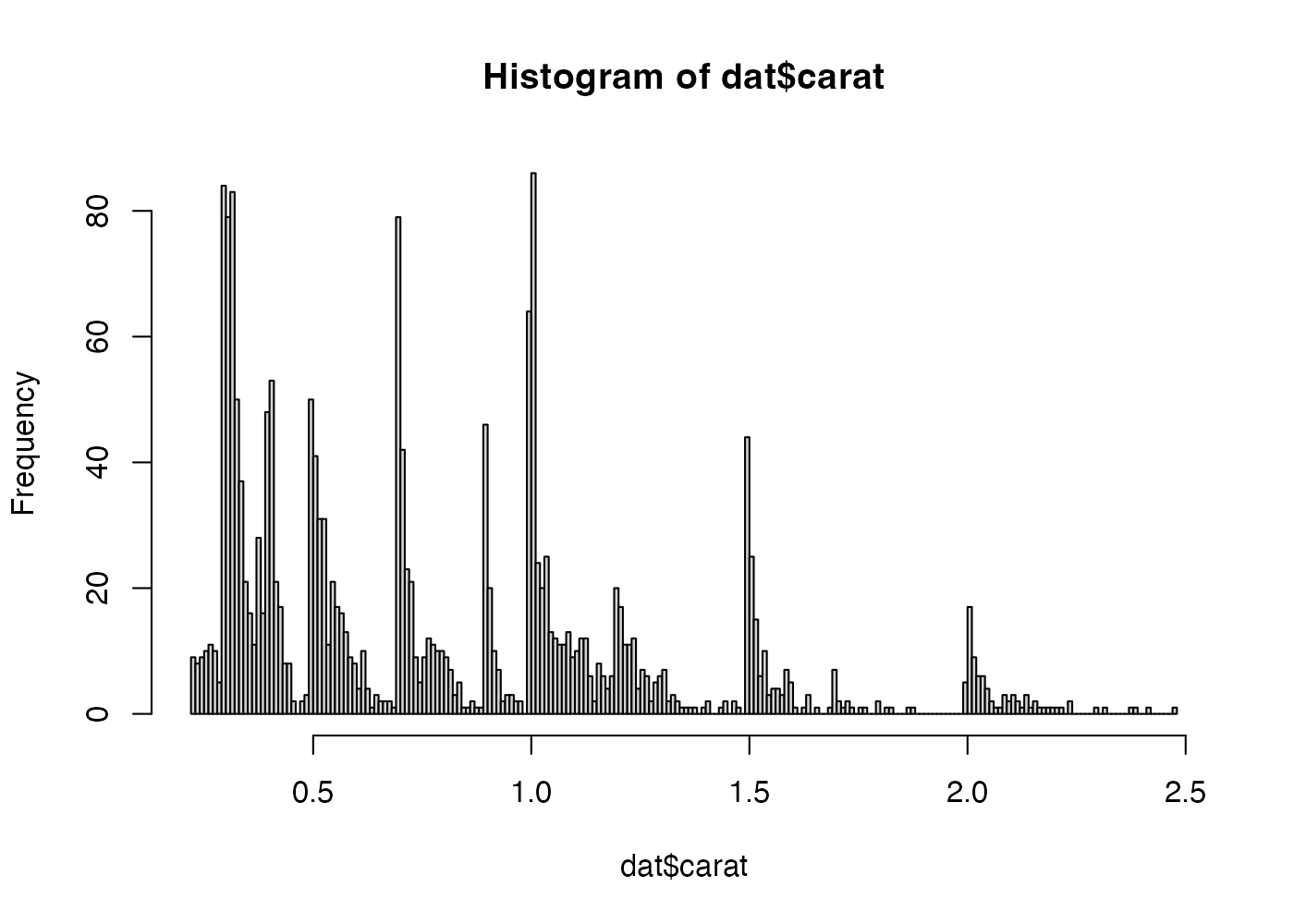
棒の数を増やした(つまり、ビン幅を小さくした)結果、カラットの分布がより詳細に明らかになりました。単純な右下がりではなく、一定の間隔でピークが繰り返し発生していることがわかります。
よく観察すると、0.5, 0.7, 1.0, 1.5, 2.0 など、キリのいい数字のところでピークが発生していることがわかります。ダイヤモンドは 0.99 カラットと 1.00 カラットで価格が大き変わります。そのため、研磨職人は原石を削る際に多少形を犠牲にしてでもキリのいい数字を下回らないよう努力します。このようなバイアスが入る結果、カラットの分布がこのようなギザギザの形状になったと考えられます。
このように、ヒストグラムはデータの分布を確認するための効率的な方法です。ヒストグラムを使う際は、ビン幅をデフォルトのままにするのではなく、適切な値に調整することで分布形状の特徴を見逃さないようにすることが重要です。
なお、ggplot2 を使ってヒストグラムを作成する際は、binwidth 引数を使ってビン幅を指定します。
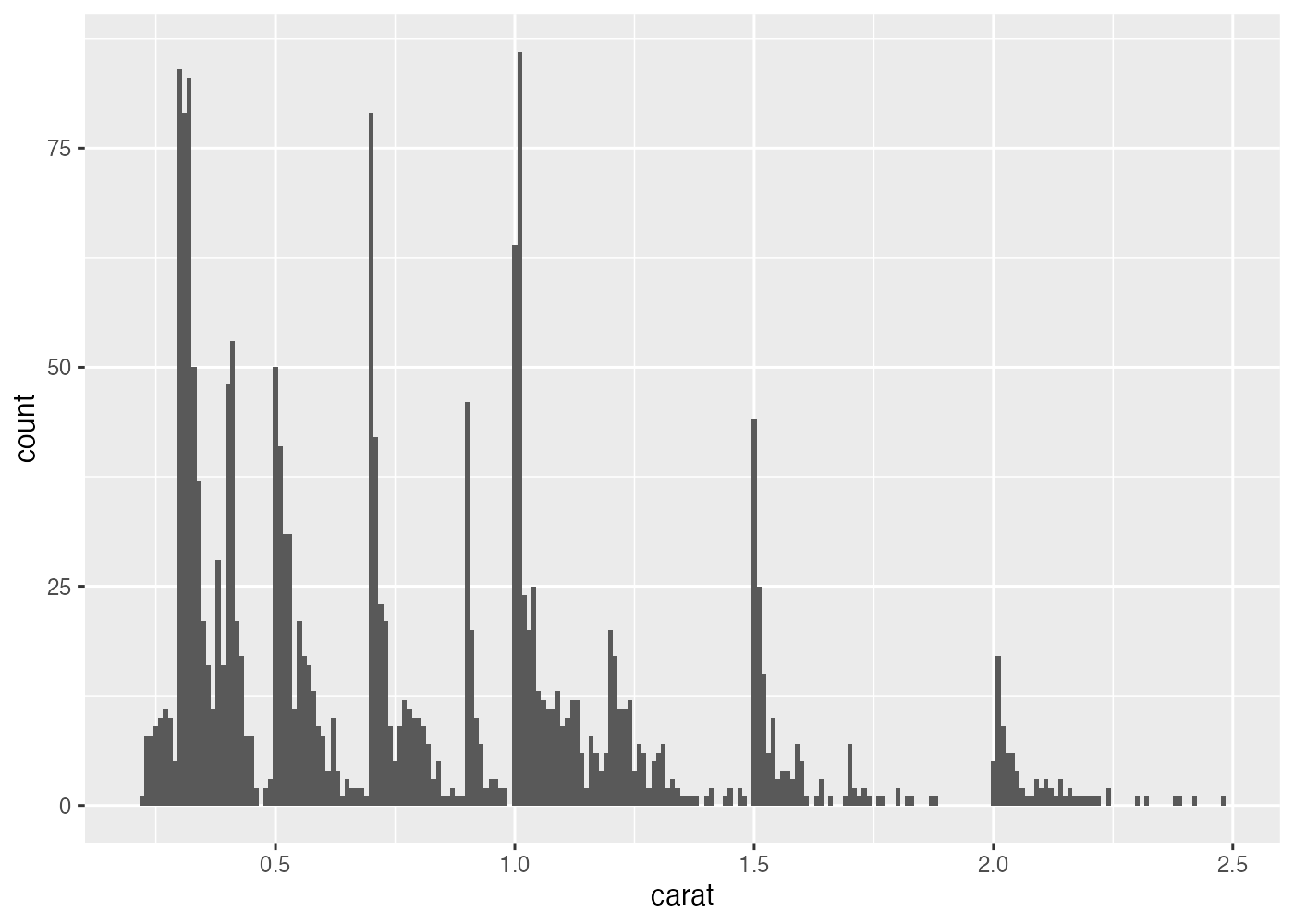
9.4.3 図の情報を増やす:棒グラフからRaincloud Plotへ
データを可視化する際、多くの人が「平均値の棒グラフ」を選びがちです。しかし、もっといいやり方があります。
ここからは、同じデータを使いつつ、可視化の方法を棒グラフから段階的に改善していきましょう。ダイヤモンドデータのカットの質(cut)ごとの価格(price)を比較します。
段階1:情報不足な「棒グラフ+エラーバー」
平均値を「棒の高さ」で、標準偏差(ばらつき)を「エラーバー」で表現しています。この形式のグラフは「ダイナマイトプロット」とも呼ばれ(形がダイナマイトに似ているから)、よく見かけるグラフです。
# 平均値と標準偏差を棒グラフで表示(stat_summaryを使用)
ggplot(dat, aes(x = cut, y = price)) +
stat_summary(fun = "mean", geom = "bar", fill = "gray70", width = 0.5) +
stat_summary(fun.data = "mean_sdl", fun.args = list(mult = 1),
geom = "errorbar", width = 0.2, linewidth = 0.5) +
theme_classic()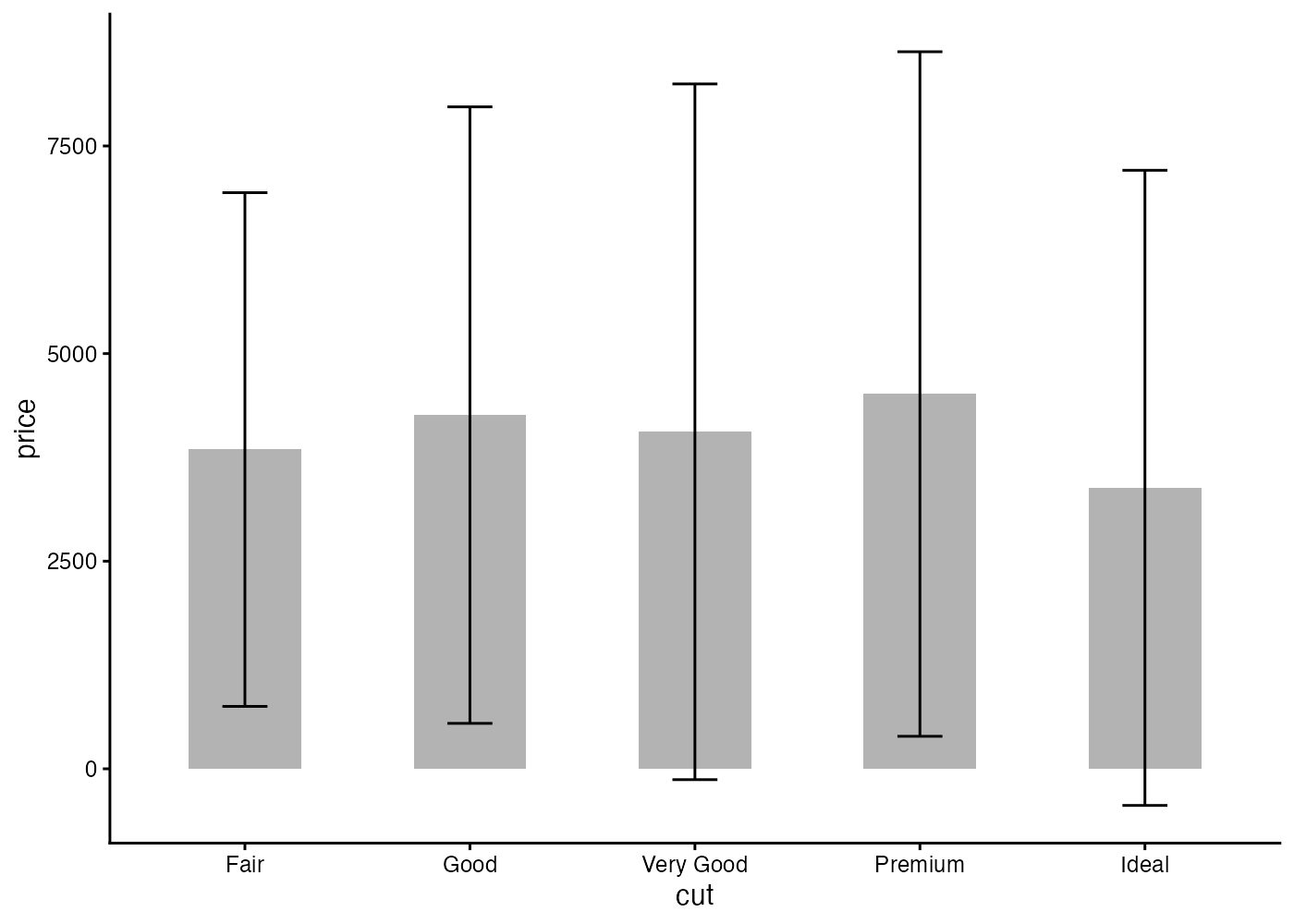
標準偏差のエラーバーを描く際はfun.data = "mean_sdl", fun.args = list(mult = 1), geom = "errorbar"を決まり文句として入れます。mult = 1 の箇所は「1標準偏差分の長さのエラーバーにする」という指定です(デフォルトでは2)。
問題点:このグラフはシンプルでわかりやすいですが、「データがどのような形で分布しているか」という情報が欠落しています。元のデータは分布が二峰性かもしれないし、極端な外れ値があるかもしれませんが、この図からはそういった情報が一切読み取れません。データの詳細を隠してしまうため、近年のデータ分析ではこのようなグラフは推奨されない傾向にあります。
段階2:生データを重ねる「ジッタープロット」
「隠されているなら、全部表示すればいい」という発想です。 平均値(点)とエラーバーに加え、背景に geom_jitter() を使って、すべての生のデータ点を散らして表示します。
なお、平均値の値についても、棒の高さではなくシンプルな点で表現する方が良いでしょう。
ggplot(dat, aes(x = cut, y = price)) +
geom_jitter(width = 0.2, alpha = 0.4, color = "skyblue") +
stat_summary(
fun.data = "mean_sdl", fun.args = list(mult = 1),
geom = "pointrange", color = "steelblue", size = 1, linewidth = 1.2) +
theme_classic()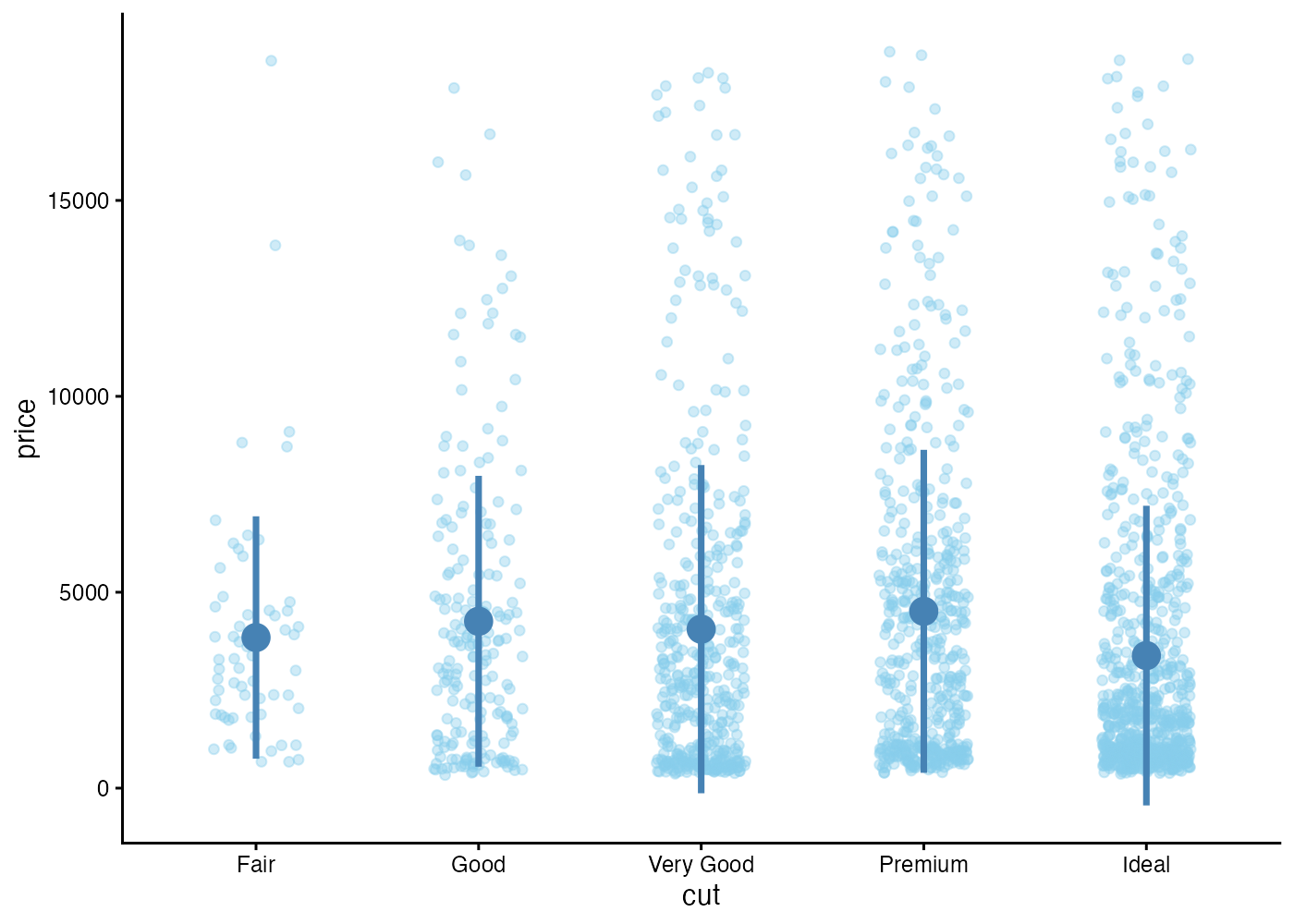
生データ(ローデータ)を表示したことで、衝撃の事実がわかります。
- データの多くは価格の低い部分(下の方)に密集している。
- 平均値(大きな青丸)は、データが密集している場所よりもかなり高い位置にある(つまり、高額な外れ値によって平均値が引き上げられている)。
ダイナマイトプロットからではこうしたデータの実態に全く気づけませんでした。
段階3:分布と要約を統合する「箱ひげ図+ジッター」
平均値・標準偏差(正規分布を前提とした指標)の代わりに、よりロバストな指標(中央値と四分位数)を表示する「箱ひげ図」を使います。
なお、ここの箱ひげ図ではoutlier.shape = NAを指定することで外れ値の点を描画しないようにしています。
ggplot(dat, aes(x = cut, y = price)) +
geom_jitter(width = 0.2, alpha = 0.5, color = "skyblue") +
geom_boxplot(outlier.shape = NA, fill = "steelblue", alpha = 0.7, width = 0.1) +
stat_summary(fun = "mean", geom = "point", color = "yellow", size = 2) +
theme_classic()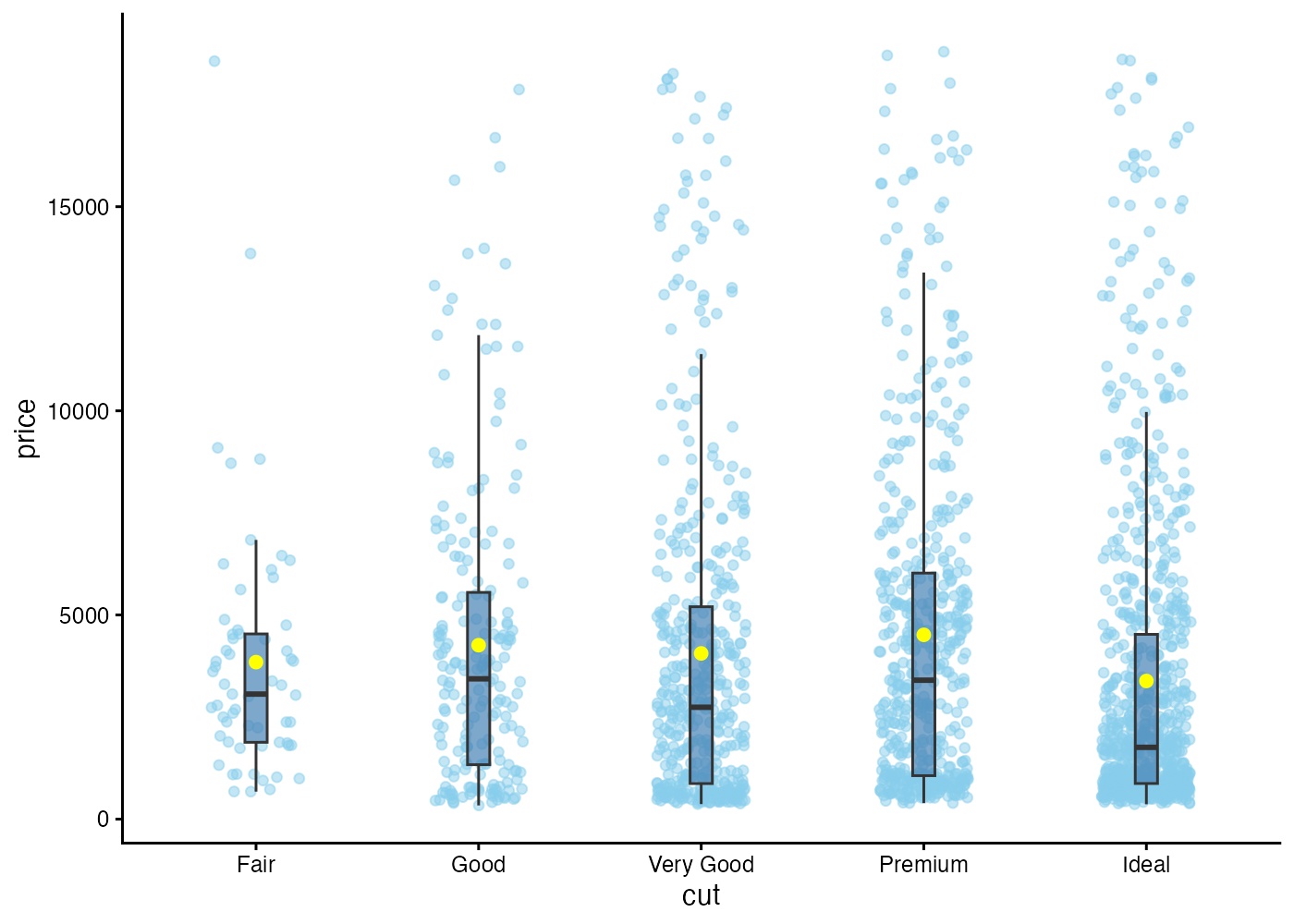
これはデータの概要把握において非常にバランスの良い可視化です。個々の生データを表示させつつ、箱ひげ図によって分布の特徴を適度に要約した情報も確認できます。
なお、箱ひげ図では通常は平均値は表示しませんが、ここでは平均値も黄色い丸で表示させています。中央値(箱の中の黒い横線)は生データの密集箇所に近い位置にあるのに比べて、平均値は上側に寄っていることが見て取れます。
最終段階:最強の可視化「Raincloud Plot」
近年、科学研究(心理学や神経科学など)の分野では Raincloud Plot(レインクラウド・プロット) と呼ばれる可視化手法がよく使われるようになってきています。
これは以下の3つを結合させたもので、雨雲(雲、雨、傘)のように見えることから名付けられました。
- 雲 (Cloud): 密度プロット(分布の形、バイオリンプロットの半分)
- 雨 (Rain): ジッタープロット(個別のデータ点)
- 傘 (Umbrella): 箱ひげ図(要約統計量)
Raincloud プロットを作成するためのパッケージは複数ありますが、ここでは ggrain パッケージを使うことにします。geom_rain() という関数ひとつで、雲(半分のバイオリン)、雨(点)、傘(箱ひげ)を自動的に綺麗に配置してくれます。
# パッケージのインストール(初回のみ)
# install.packages("ggrain")
library(ggrain)
ggplot(dat, aes(x = cut, y = price, fill = cut)) +
geom_rain(alpha = 0.3) +
theme_classic() +
theme(legend.position = "none") # 色の凡例は不要なので消す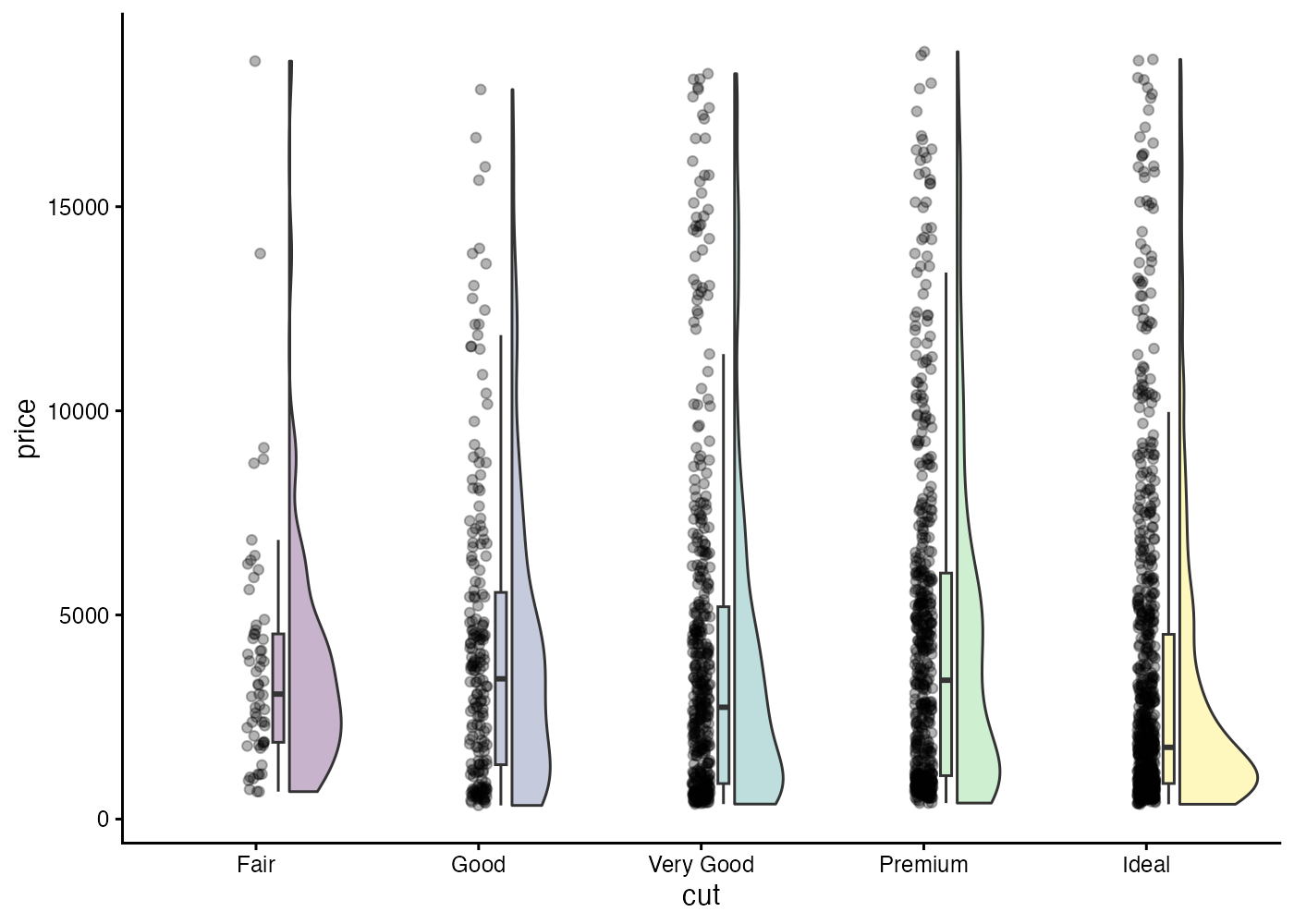
このグラフを見れば、「どこに山(データの密集箇所)があるか」「裾がどこまで伸びているか」「中央値はどこか」「外れ値はどれくらいあるか」という全ての情報を、一枚の図で伝えることができます。
最初の棒グラフとこの図を比較してみてください。同じデータなのに、可視化の方法次第で伝えられる情報の豊富さ(そして、データに対する理解の深まり)に非常に大きな差が生じることがよくわかると思います。
なお、Raincloud プロットは情報が多い(あるいは多過ぎてややこしい)ので、実用上は段階2や段階3のグラフでも十分だという場合も多いかもしれません。それらのグラフでも、最初の棒グラフに比べればデータの分布の特徴を豊かに伝えてくれています。
雨雲プロットは向きを変えて描かれることも多いです。
ggplot(dat, aes(x = cut, y = price, fill = cut)) +
geom_rain(alpha = 0.3, cov = "cut") + # cov で点に色をマッピング
theme_classic() +
coord_flip() + # 軸の入れ替え
theme(legend.position = "none")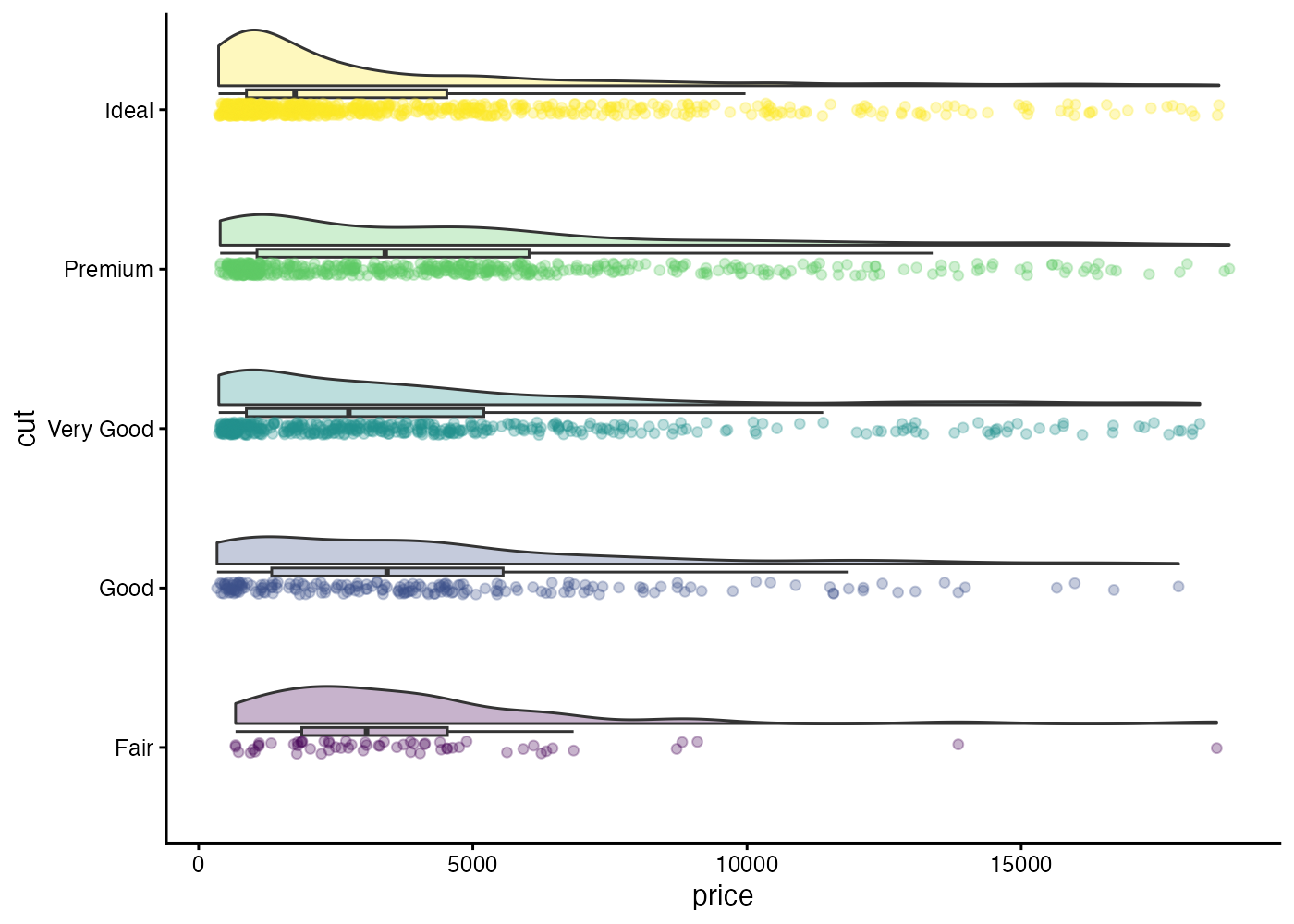
この向きで描いた方が雨雲っぽさがより出ますね。
ggrain パッケージの詳しい使い方は以下のページを参照してください。
https://cran.r-project.org/web/packages/ggrain/vignettes/ggrain.html
9.5 まとめ
このページではデータの概要と分布を把握することの重要性を説明しました。
1. まずは記述統計から
- 平均値・標準偏差、度数分布などの要約統計量を算出し、データの傾向を知る。
- table(), summary(), psych::describeBy(), aggregate()
2. 数値だけで安心しない
- 要約統計量が同じでもデータの構造が別物であることがある。
- 平均値は外れ値に弱いし、多峰性分布(二つの山)の場合は谷間を示してしまう。
3. 分布を可視化する
- 単なる棒グラフでは分布の情報が隠されてしまう。
- ヒストグラムや箱ひげ図、雨雲プロットの利用、そして生データの表示などによって、データの分布形状を詳細に表現できる。
9.6 発展的問題
9.6.1 タイタニック号の乗客の生存率
タイタニック号が沈没する際、船長は女性と子供を優先的に避難させるように指示したと言われています。その結果を検討するため、性別と年齢層ごとの生存率を計算してください。さらに、客室クラスの影響も含めた集計も行ってください。
ヒント:特定の年齢を境にして乗客を子供と大人の2つに分け、その分類を示す列をデータに追加し、それをグループにして集計をするとよい。
解答と解説(クリックして展開)
dat = titanic::titanic_train
# 年齢データのない行は分析から省く
df = subset(dat, !is.na(Age))
# 10歳未満を子供としてカテゴライズする
df$Generation = ifelse(df$Age < 10, "Child", "Adult")
# 集計の実施
aggregate(Survived ~ Generation + Sex + Pclass, data = df, FUN = mean)
## Generation Sex Pclass Survived
## 1 Adult female 1 0.97619048
## 2 Child female 1 0.00000000
## 3 Adult male 1 0.38383838
## 4 Child male 1 1.00000000
## 5 Adult female 2 0.90909091
## 6 Child female 2 1.00000000
## 7 Adult male 2 0.06666667
## 8 Child male 2 1.00000000
## 9 Adult female 3 0.44444444
## 10 Child female 3 0.52380952
## 11 Adult male 3 0.12931034
## 12 Child male 3 0.38095238
# dplyr版
df %>%
group_by(Pclass, Sex, Generation) %>%
summarise(
Survived.Mean = mean(Survived, na.rm = TRUE),
N = n(),
.groups = "drop"
)
## # A tibble: 12 × 5
## Pclass Sex Generation Survived.Mean N
## <int> <chr> <chr> <dbl> <int>
## 1 1 female Adult 0.976 84
## 2 1 female Child 0 1
## 3 1 male Adult 0.384 99
## 4 1 male Child 1 2
## 5 2 female Adult 0.909 66
## 6 2 female Child 1 8
## 7 2 male Adult 0.0667 90
## 8 2 male Child 1 9
## 9 3 female Adult 0.444 81
## 10 3 female Child 0.524 21
## 11 3 male Adult 0.129 232
## 12 3 male Child 0.381 21
- 子供の生存率は大人よりも高いことがわかります。
- 1等客席の女性の子供の生存率が0%ですが、これはそのグループに1人しか該当者がいないので例外的な値です。
9.6.2 まとめ買いキャンペーンの効果
あなたはとある通販サイトのマーケティング担当者です。このサイトでは現在、「5000円以上のお買い上げで送料無料!」というキャンペーンを実施しています。このキャンペーン実施中の販売データを分析すると、平均購入単価(客単価)は約4700円ほどで、5000円には届いていませんでした。このキャンペーンは失敗しているのでしょうか?
以下のスクリプトを実行して販売データ dat を作成し、キャンペーンの効果を分析してください。
set.seed(123)
base_amount = rnorm(1000, mean = 4500, sd = 1500)
base_amount = round(pmax(100, base_amount))
final_amount = sapply(base_amount, function(x) {
if (x >= 4000 && x < 5000 && runif(1) < 0.8) {
return(x + 1000 + rnorm(1, 0, 100))
} else {
return(x)
}
})
dat = data.frame(Amount = round(final_amount))解答と解説(クリックして展開)
library(tidyverse)
# 平均購入額の確認
print(mean(dat$Amount))
## [1] 4739.182
# ヒストグラムで売上の分布を可視化
ggplot(dat, aes(x = Amount)) +
geom_histogram(binwidth = 100, fill = "orange", color = "white") +
geom_vline(xintercept = 5000, color = "blue", linetype = "dashed", size = 0.7) +
scale_x_continuous(limits = c(0, 10000), breaks = 1000 * 0:10) +
theme_minimal()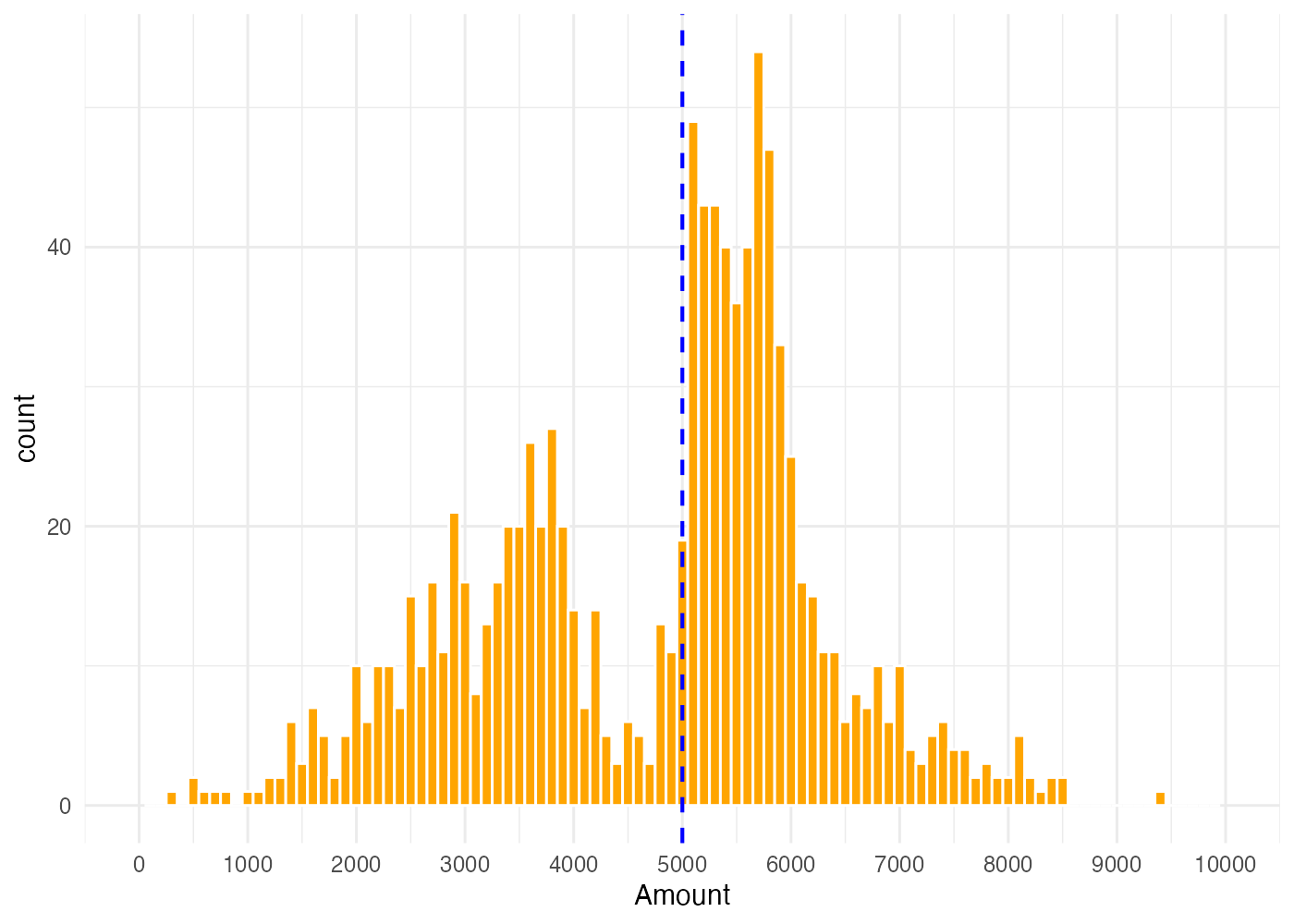
- ヒストグラムを見ると5000円を境に谷と山ができています。
- 4000円台の客が買い増しして5000円台の購入額になっているせいでこのような分布形状になっていると考えられます。したがって、キャンペーンは確かに効果的であることがわかります。
- 平均値が5000円に届かないのは購入金額が少ない客が多くいるからです。
# 密度プロットの場合
ggplot(dat, aes(x = Amount)) +
geom_density(fill = "orange", alpha = 0.5, adjust = 0.2) +
geom_vline(xintercept = 5000, color = "blue", linetype = "dashed", size = 0.7) +
scale_x_continuous(limits = c(0, 10000), breaks = 1000 * 0:10) +
theme_minimal()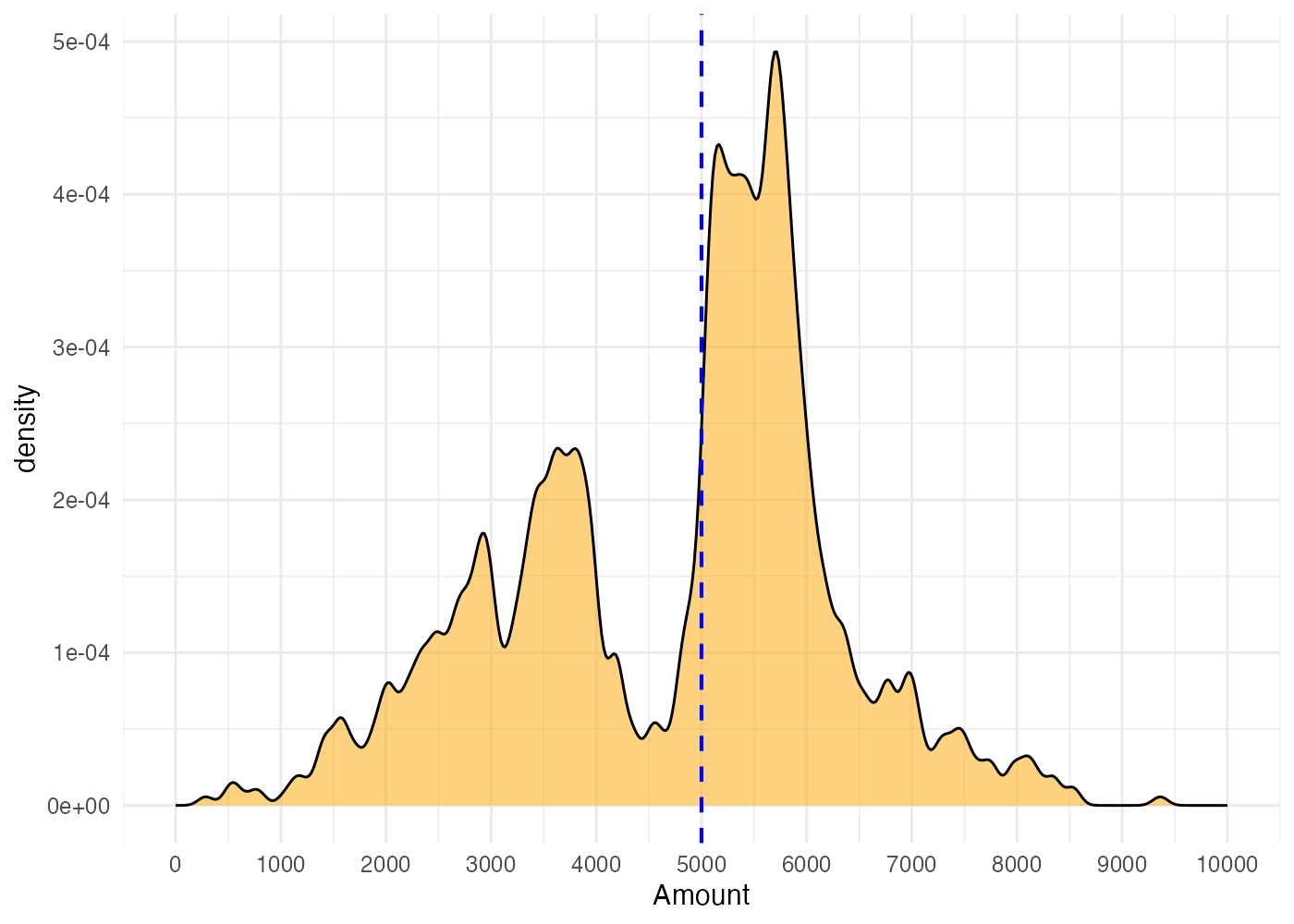
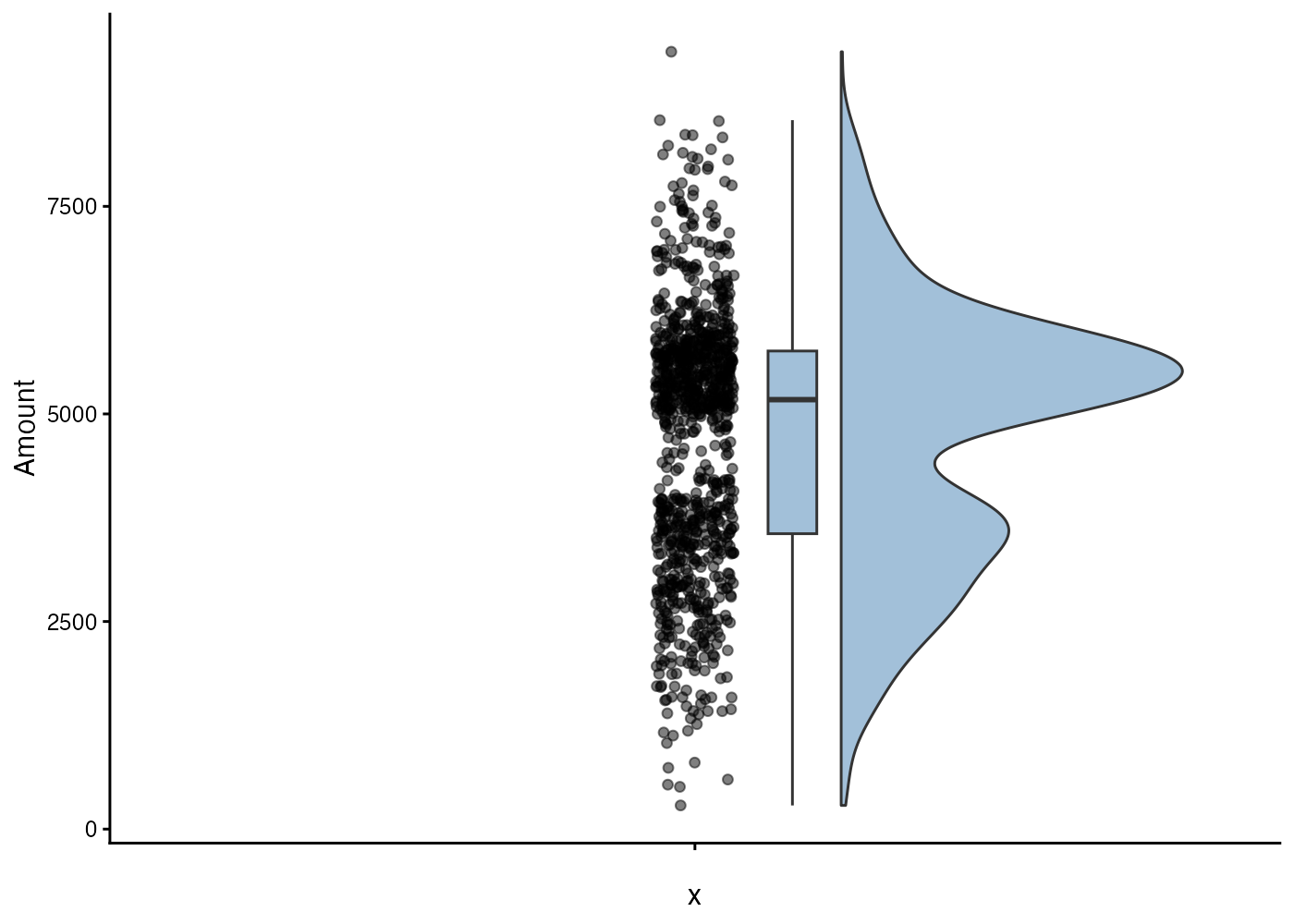
# 雨雲プロットの場合
# aesでxとyの両方を指定しないとエラーになるので、xにはダミーのグループを指定する
ggplot(dat, aes(x = "", y = Amount)) +
ggrain::geom_rain(alpha = 0.5, fill = "steelblue") +
theme_classic()